Матрица преобразований

Матрица преобразований применяется для вычисления новых координат объекта при его трансформации. Изменяя значения элементов матрицы преобразования, к объектам можно применять любые трансформации (например: масштабирование, зеркальное отражение, поворот, перемещение и т. п.). При любой трансформации сохраняется параллельность линий объекта.

Координаты в PDF выражаются в терминах двумерного пространства. Точка (x, y) в пространстве может быть выражена в векторной форме [x y 1]. Постоянный третий элемент этого вектора (1) нужен для использования вектора с матрицами 3х3 в вычислениях, описанных ниже.

Преобразование между двумя системами координат представлено, как матрица 3х3 и записывается следующим образом:

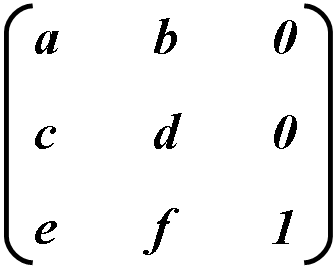
Координатные преобразования выражаются в виде матричных умножений:

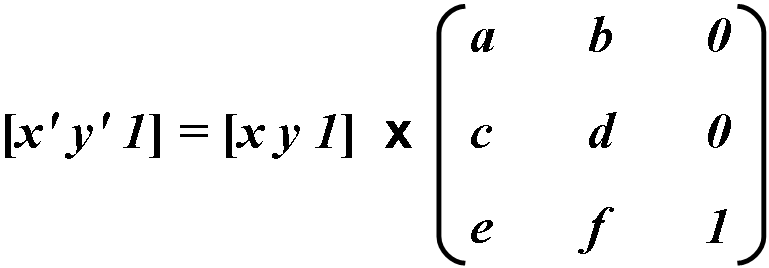
Так как последняя колонка не оказывает ни какого влияния на результаты расчета, то она в вычислениях не принимает участия. Координаты трансформации высчитываются по следующим формулам:

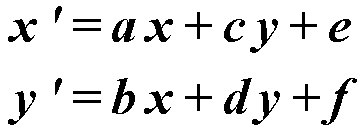
Единичная матрица

Единичной матрицей называется, та у которой значения матрицы a и d равны 1, а остальные равны 0. Такая матрица применяется по умолчанию, так как не приводит к трансформации. Поэтому единичную матрицу используют как основу.

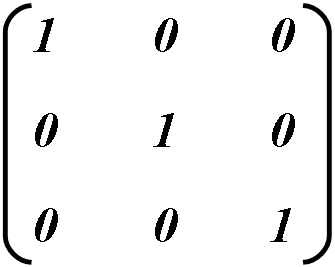
Масштабирование

Для увеличения или уменьшения размера объекта по горизонтали/вертикали следует изменить значение a или d соответственно, а остальные применить из единичной матрицы.

Например: Для увеличения размера объекта в два раза по горизонтали, значение a необходимо принять равным 2, а остальные оставить такими как в единичной матрице.

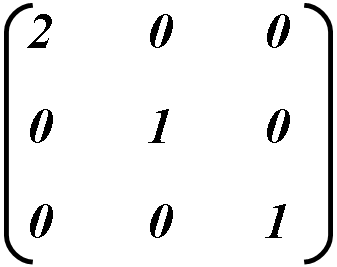
Высчитываем новые координаты объекта:

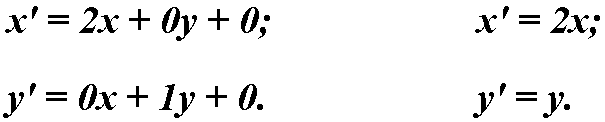
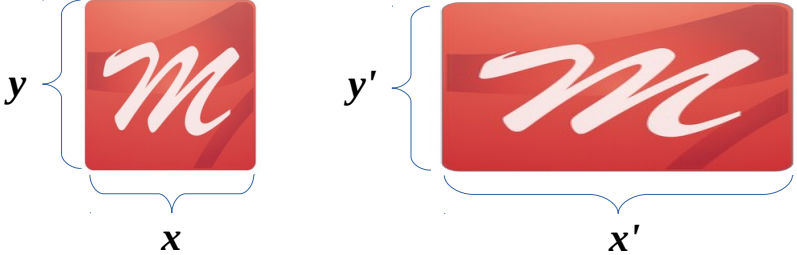
Отражение

Чтобы получить зеркальное отображение объекта по горизонтали следует установить значение a = -1, по вертикали d = -1. Изменение обеих значений применяется для одновременного отображения по горизонтали и вертикали.

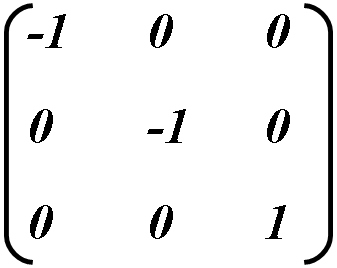
Наклон

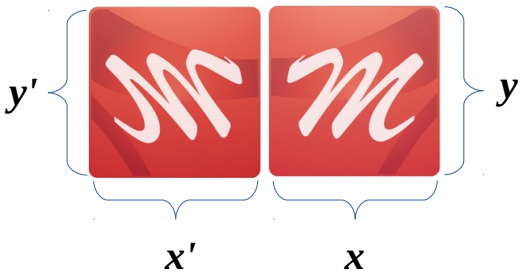
Наклон объекта по вертикали/горизонтали обеспечивается изменением значений b и c соответственно. Изменение значения b/-b — наклон вверх/вниз, c/-c – вправо/влево.

Например: Для наклона объекта по вертикали вверх установим значение b = 1

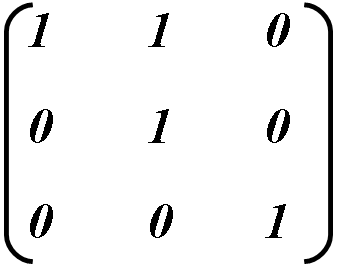
Высчитываем новые координаты объекта:

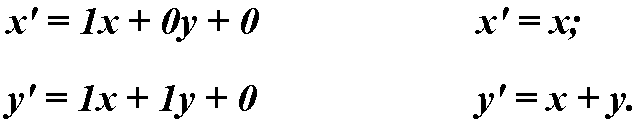
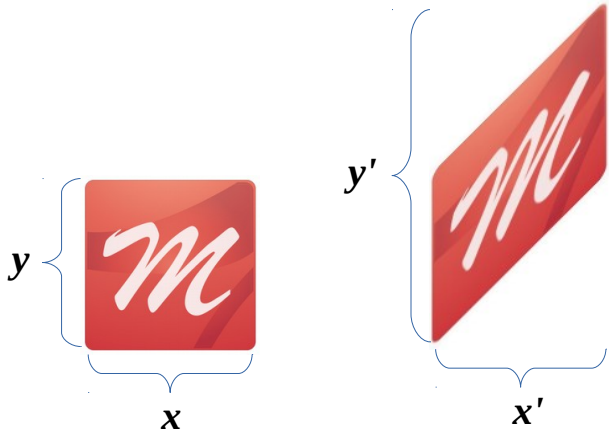
В итоге к наклону объекта приводит только координата y, которая увеличивается на значение x.

Поворот

Поворот — это комбинация масштабирования и наклона, но для сохранения начальных пропорций объекта, преобразования должны проводится с точными вычислениями при использовании синусов и косинусов.

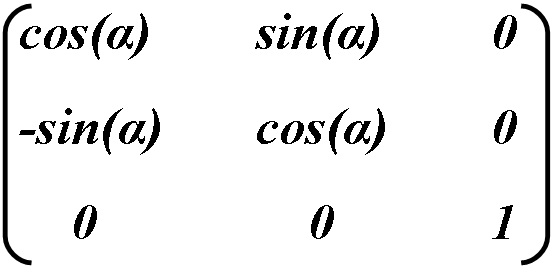
Сам поворот происходит против часовой стрелки, α задаёт угол поворота в градусах.

Перемещение

Перемещение осуществляется изменением значений e (по горизонтали) и f (по вертикали). Значения задаются в пикселях.

Например: Перемещение с использованием матрицы применяется редко из-за того, что эту операцию можно проделать другими методами, например, изменить положение объекта во вкладке Геометрия.

Поскольку матрица трансформации имеет только шесть элементов, которые могут быть изменены, визуально она отображается в PDF [a b c d e f]. Такая матрица может представлять любое линейное преобразование из одной координатной системы в другую. Матрицы преобразований образуются следующим образом:

Перемещения указываются как [1 0 0 1 t_x t_y], где t_x и t_y — расстояния от оси системы координат по горизонтали и вертикали, соответственно.
Масштабирование указывается как [s_x 0 0 s_y 0 0]. Это масштабирует координаты так, что 1 единица в горизонтальном и вертикальном измерениях в новой координатной системе такого же размера, как и s_x и s_y единиц в старой координатной системе соответственно.
Повороты производятся матрицей [cosθ sinθ −sinθ cosθ 0 0], что соответствует повороту осей координатной системы на θ градусов против часовой стрелки.
Наклон указывается как [1 tanα tanβ 1 0 0], что соответствует наклону оси x на угол α и оси y на угол β.

На рисунке ниже показаны примеры трансформации. Направления перемещения, угол поворота и наклона, показанные на рисунке, соответствуют положительным значениям элементов матрицы.

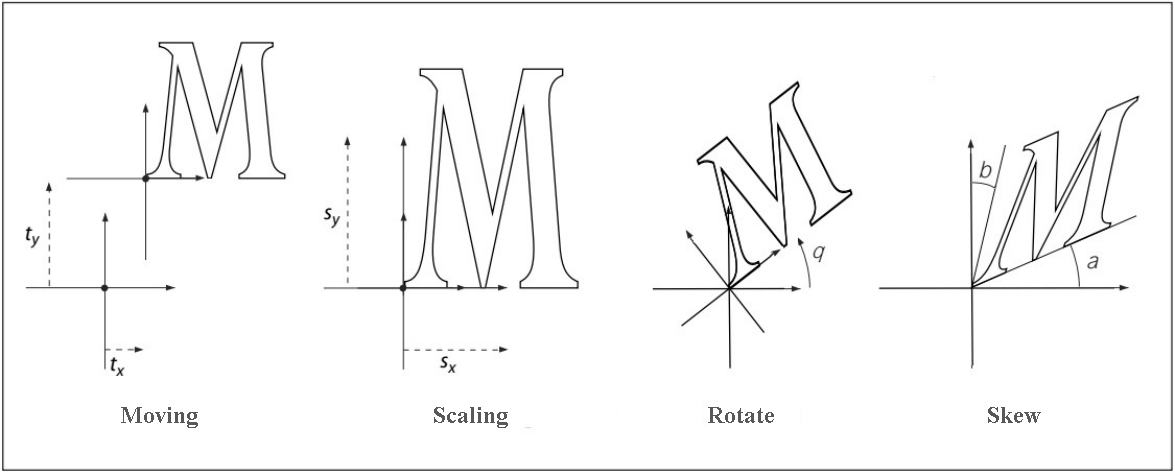
Умножения матрицы не коммутативны — порядок, в котором перемножаются матрицы, имеет значение.

В таблице ниже приведены допустимые преобразования и значения матрицы.

Исходный рисунок	Трансформированный рисунок	Матрица	Описание
		1 0 0 2 0 0	Масштаб по вертикали. Если значение матрицы больше 1, объект расширяется, меньше 1 — сжимается.
		2 0 0 1 0 0	Масштаб по горизонтали. Если значение матрицы больше 1, объект расширяется, меньше 1 — сжимается.
		-1 0 0 1 0 0	Отражение по горизонтали.
		1 0 0 -1 0 0	Отражение по вертикали.
		1 1 0 1 0 0	Наклон по вертикали вверх.
		1 -1 0 1 0 0	Наклон по вертикали вниз.
		1 0 1 1 0 0	Наклон по горизонтали вправо.
		1 0 -1 1 0 0	Наклон по горизонтали влево.
		1 0 0 1 0 1	Смещение по вертикали вверх в пикселях.
		1 0 0 1 0 -1	Смещение по вертикали вниз в пикселях.
		1 0 0 1 1 0	Смещение по горизонтали вправо в пикселях.
		1 0 0 1 -1 0	Смещение по горизонтали влево в пикселях.

Несмотря на все выше сказанное, матрица преобразований очень простой и эффективный инструмент для трансформации. Конечно, применять ее, например, для поворота нецелесообразно, так как во вкладке Геометрия имеется функция Поворот, но для отражения объекта она просто необходима.